統計の初歩(分散/標準偏差/相関係数の計算)
分散と偏差の計算
データのちらばり具合を定量的に評価するための基礎データを計算してみる.プログラムは先に作成したマクロ中に必ず追記すること.- まずはじめに,Excelシート中の表1の右側に並んでいる統計データの最小値,最大値,平均値(相加平均)を計算するプログラムを追記する.ここでは,ワークシート関数,MAX(),MIN(),AVERAGE()を使用することとする.詳細は,図の下にある参考資料を確認すること.関数の使用に当たっては,セルの指定方法に注意すること.
- 計算結果はO6〜O8のセルに出力すること.下の図と比較して計算結果が正しいかを確認しておくこと.

参考資料:「ワークシート関数の呼び出し」 「Excel関数について」 「データ処理で使用される関数」 - 平均値を基準としたちらばり具合を意味する偏差(身長−クラスの平均身長)を個々に計算して,Excelシート中のC列に出力させる.
- このクラスの散らばり具合を表す代表値を示すため,先に計算した偏差の合計値を総度数で除して平均化したいところだが,ゼロになるため,各個人の偏差を2乗した値の合計を求めて,総度数で除した分散を計算する.
- 分散の計算結果をO9のセルに出力して,「31.5・・・」になっているかを確認してみる.
標準偏差と相関係数の計算
続いて,このクラスの身長と体重のちらばり具合と相関性について定量的に評価してみる.体重のプログラムのEnd subの下側に新しいプログラムを記述して,[相関係数計算]ボタンに登録すること.- マクロは,先に作成したマクロ標準モジュール1の End Sub の次の行に Sub プログラム名()〜End subを記述してできる領域(線で区切られる)で行うこと.
- 分散の平方根で表される標準偏差を身長と体重それぞれで計算し,Y14,Y15のセルに出力する.平方根を求める場合は,Sqr(変数または数値)関数を使用すること.
- 計算結果が身長の標準偏差「5.612・・・」,体重の標準偏差「8.950・・・」となっているかを確認する.
- 計算結果から身長と体重のどちらがばらつきが大きいと言えるかをイメージする.
- 各個人の身長の偏差と体重の偏差を乗じたものをF列に出力する.For〜Nextで50回計算すると良い.
- F列の合計値を人数で除した共分散を計算し,Y16のセルに出力する.ここで求めた共分散は,2種類のデータ間の関係の強さを表す数値である.合計値の計算はワークシート関数を用いても良い.
- 共分散を身長の標準偏差と体重の標準偏差で除した相関係数をY17のセルに出力する.身長と体重の相関性について,下記を参考にどのような評価をすることが適切かイメージしておくこと.
| -1.000〜-0.600 高い負の相関 | +0.200〜+0.399 低い正の相関 | -0.599〜-0.400 中位の負の相関 | +0.400〜+0.599 中位の正の相関 |
| -0.399〜-0.200 低い負の相関 | +0.600〜+1.000 高い正の相関 |
| -0.199〜+0.199 無相関 |
計算結果の検証
- 適当な空白セルに標準偏差を計算するためのワークシート関数=STDEVP(B4:B53またはD4:D53)を挿入して,VBAの計算結果と等しくなるか確認する.
- 適当な空白セルに相関係数を計算するためのワークシート関数=CORREL(B4:B53,D4:D53)を挿入して,VBAの計算結果と等しくなるか確認する.
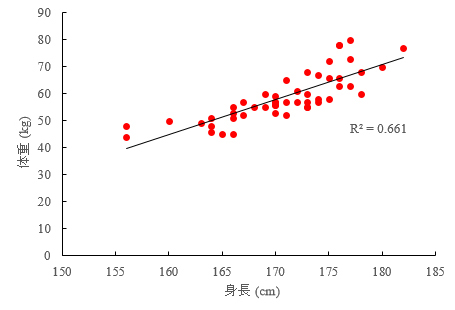
- 横軸に身長と縦軸に体重の散布図をシートの適当な位置に作図する.ここでは,グラフのフォーマットを適当にしても良い.
- 散布図のプロット上で右クリックし,「近似曲線の追加(線形近似)」を選択,「グラフにR-2乗値を表示」にチェックマークを入れる.
- グラフ中に表示されたR-2乗値と,Y17のセルに出力した値を2乗したものが同じになるかを確認する.ちなみに,この関係は線形近似のときだけに適用される.ExcelのR-2乗値(決定係数という)と相関係数は異なるものなので,今後の研究活動においては,両者の意味合いを混同しないように注意すること.
スペシャル問題
- シート内に[データクリアー] ボタンを追加し,計算させた全てのデータを消去できるようにする.(難易度:★)
- 身長と体重それぞれの偏差の合計がゼロになることをプログラム上で確認する.(難易度:★)
- セルの書式を設定する方法を調べて,計算結果の小数点桁数を揃える(桁数は自由).(難易度:★★)
- 身長と体重の刻み量(O4,Y4のセル)を変化させた時に,自動で階級が変化して統計処理できるようにする.(難易度:★★★)
トップページに戻る