MECHANIZUM OF FAILURE
Figure 14 shows the variation in the net minimum principal stress, (σ3-ua ), with the shear strain, εs , in lower net stress. It is interesting that when (σ3-ua ) falls to zero or slightly below zero and reaches the lowest peak, the failure occurs in each case. In other words, when the specimen is subjected to tensile stress, the failure, which is similar to a brittle fracture, may occur immediately. It means that the strength barely increases with matric suction under tensile stress conditions.
The photographs of failure planes are presented in Figs. 15 and 16, which are the case of higher net stress (pnet =200kPa, s =400kPa) and lower net stress (pnet =50kPa, s =400kPa), respectively. As the direction of σ1 leans to the horizontal direction from the vertical axis by 45 degrees (α =45o) in this experiment, the angle of failure plane from the horizontal ought theoretically to be φ/2 on the basis of Mohr-Coulomb's failure criterion(see Fig. 17. In Fig. 15, the angle of failure plane is approximately 20 degrees which is supposed to be close to φ/2, while the angle is about 40 degrees in Fig. 16. As the angle is 45 degrees when tensile failure occurs, the failure in Fig. 16 implies being close to tensile failure. Therefore, it can be interpreted that tensile failure is induced in low net stress, although shear failure occurs in higher net stress.
Figure 18 illustrates the new failure criterion in consideration of tensile failure. If it is assumed that the failure occurs when (σ3-ua ) becomes zero, this leads to the following equation in these test conditions.
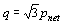
This equation agrees with those obtained from the experiment in low net stress (Fig. 18). Although there is the strength to bear small tensile stress on unsaturated soils exactly, it is so small that it may be able to ignore the tensile strength on practical problems. The new failure criterion, which is the condition of (σ3-ua ), is proposed on lower net stress, where tensile failure has to occur. The general failure lines on unsaturated soils are attained by addition of the new failure lines to the existing failure lines. However, special attention should be paid to the tensile strength, which may have a significant increase in higher matric suction, as the strength slightly increase with matric suction in the tensile failure region (Fig. 18).
The same relationships as Fig. 18 are shown in Fig. 19 with respect to the minimum q after the failure and the higher net stress. In this state, the difference among the failure lines with respect to matric suction is almost negligible and the failure lines tend to converge in one line, which is contrary to our knowledge. It might indicate that the mechanical effect of matric suction changes after the failure plane is formed.
RETURN