EXPERIMENTS
Apparatus
There are several problems concerning stress and strain non-uniformity occurring across the wall of a hollow-cylindrical specimen. These problems were pointed out by Hight et al. (1983) as follows:
1. Variations in radial stress σr and circumferential stress σθ across the wall due to differences between inner cell pressure pi and outer cell pressure po .
2. Variations in shear stress σzθ and shear strain εzθ across the wall due to curvature.
3. Stress and strain non-uniformity due to end restraint.
To minimize the effect of stress and strain non-uniformity, it is necessary that the ratio of the inner and outer diameters (di / do ) should approach the value of 1 and that the height be nearly twice the outer diameter do (Tatsuoka et al., 1986). Therefore, in order to reduce the stress and strain non-uniformity and to effectively use the existing triaxial cell in the experiments, the size of the specimen was expanded from the former size of di = 30mm, do = 70mm and h = 100mm to the new size of di = 50mm, do = 80mm and h = 160mm.
The triaxial cell of the apparatus is represented schematically in Fig. 1. The apparatus was improved so that experiments with partially saturated soils would be made possible by using a double-walled triaxial cell. The changes in the inner and outer diameters are calculated through the volume changes, which are measured by differential pressure transducers (DPT) in the hollow cylinder and inner cell, respectively (Fig. 1). The axial displacement and the rotational angle are measured outside the triaxial cell. The load cell, in which the influence of cell pressure is almost negligible and which can measure the torque and axial load, was installed inside the triaxial cell to remove the effect of rod friction on the measurement.
In the hollow-cylindrical torsional shear apparatus, four stresses (vertical stress σz , radial stress σr , circumferential stress σθ and shear stress σzθ ) can be controlled independently. However, it is difficult to control these four stresses precisely via a manual control. Therefore, an automatic control system using a personal computer was introduced to improve the accuracy and stability, and to reduce labour. The concept of automatic measurement and control for the apparatus is shown in Fig. 2.
Samples
The cohesive lateritic soil was sampled in the Yoneyama area of Niigata Prefecture (Japan). During the air drying process, clay chunks were continuously pounded with a wooden hammer to reduce their size. The soil obtained by sieving out soil particles greater than 0.84mm was used in the experiment. The classification of this soil, based on the Japanese Unified Soil Classification System (designated as JGS), is MH and is referred to as Yoneyama sandy silt in this study. The physical properties of the soil are summarized in Table 1 and the grain size distribution is shown in Fig. 3.
The test specimens were prepared as follows. The soil and de-aired water were mixed and stirred well to make a slurry with a water content of about 80%. The pre-consolidation using this slurry was performed one-dimensionally in a mold under a vertical pressure of 45kPa. This vertical stress was chosen from the minimum vertical stress at which the specimen can keep its shape during trimming. After completing the pre-consolidation, the consolidated soil block with a water content of about 40% was taken out of the mold and its top and bottom were cut off. The hollow cylindrical specimen was made by trimming the soil block.
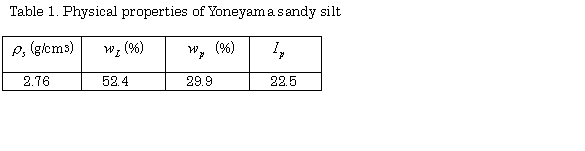
Stress and Strain Parameters
The idealized stress conditions in a hollow-cylindrical sample subjected to external forces (Fv , T ) and pressures (pi , po ) are illustrated in Fig. 4. The average values of the four stresses and four strains, namely, vertical stress σz , radial stress σr , circumferential stress σθ and shear stress σzθ ; axial strain εz , radial strain εr , circumferential strain εθ and shear strain γzθ = 2εzθ ; are calculated using the methods given by Hight et al. (1983). It was shown by Tatsuoka et al. (1986) that the effects of membrane forces were remarkable even at σc' = 98.1kPa by checking the differences between corrected and uncorrected values of σ1' / σ3' halfway down the sample. The correction for the membrane forces made by Tatsuoka et al. (1986) was therefore introduced in this research.
The stress and strain parameters used in this research are defined as follows.
Major principal stress, σ1, intermediate principal stress, σ2, and minor principal stress, σ3 :
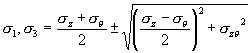
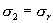
Effective mean principal stress, p' :
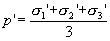
Deviator stress, q :
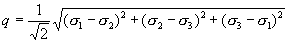
The magnitude of q during the shear history process is referred to as qh .
Direction of the major principal stress relative to the vertical axis, α:
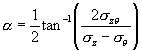
Relative magnitude of the intermediate principal stress, b :
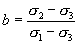
The values of α and b during the shear history and the shear are referred to as αh , bh and αs , bs , respectively.
Major principal strain, ε1, intermediate principal strain, ε2, and minor principal strain, ε3 :
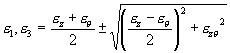
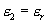
Volumetric strain, εv :
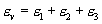
Shear (deviator) strain, εs :
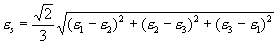
Direction of the major principal strain relative to the vertical axis, αε :
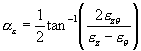
Test Procedure
The torsional shear tests were performed on the specimens which were each subjected to four processes as follows.
1. The specimen was consolidated isotoropically under a certain confining pressure p' = 100kPa. (Isotropic consolidation process)
2. After isotropic consolidation, the specimen was sheared under drained conditions with strain control. Shear stress was applied with a certain deviator stress qh under stress conditions of p' = pc' , αh = 0o, +-22.5o or +-45o, bh = 0, 0.5 or 1. (Shear history process)
3. The shear stress was unloaded to create isotropic stress conditions which were the same as the stress conditions in the isotropic consolidation process. (Unloading process)
4. Torsional shear tests, under stress conditions of p' = pc', αs = 45o, bs = 0, 0.5 or 1, were carried out under drained conditions with strain control until εs was approximately equal to 4 - 5%. (Shear process)
These four processes are illustrated in Fig. 5. The cases of different b between the shear history and the shear process are illustrated on the π plane (Fig. 6). The test without the shear history, which is subjected only to the isotropic consolidation and the shear process, is referred to as virgin shear.
A back pressure of 200kPa was applied to all specimens throughout all the processes to obtain full saturation (Skempton's B value greater than 0.98). Figure 7 shows the relationship between drained water and elapsed time during the isotropic consolidation process. From this, three hours was chosen as the consolidation time in these experiments. The rate of shear strain during the shear history and the shear process was about εs = 0.0056%/min. The shear rate and the reproductivity of the experiment were confirmed sufficiently in a preliminary experiment. The stress conditions during the shear history process and during the drained shear process are summarized in Table 2.
RETURN